mini-sglang

封面出自笔者非常喜欢的一个乐队的新专 The stars will light the way, ~~放一张飞龙在这里寓意着你也可以写一个性能非常强甚至超过 SGLang 和 vLLM 的框架~~

在 7 月初, 笔者在自己的项目中需要用到一个高性能的 LLM serving engine. 但是现有的开源 SOTA 比如 sglang, TensorRT-LLM, vllm 什么的, 过于重量级了, 笔者改起来无从下手. 于是决定了自己从头写一个 LLM 框架, 在这过程中也顺便能加深对于 serving engine 不同组件的理解. 于是就有了现在这个项目.

笔者最早是在六月最后两三天的时候开始写的, 中途因为去 OSDI 开会基本是中断了一周 (倒时差差点干死了笔者). 而且一开始这个框架也不是作为 serving engine. 总之实际花在上面的时间大约只有三周, 但是三周时间足以支持很多高性能 serving engine 所需要的核心 feature 了. 在写这个所谓 mini sglang 的过程中, 笔者自然也是参考了不少 sglang 的 codebase, 不过更多时候笔者还是自己 design, 作为一个做 system 的人, 自己 design 一个 system 再去不断 refine 才是最爽的.

废话不多说, 直接进入正题. 本文还会顺带介绍一些 LLM serving 中非常著名的 paper, 其中的 idea 现在看来并不复杂, 实现起来也没有很多细节.

Model Structure

Remark: 这部分笔者花了一周, 当然还有一些杂七杂八的 profiling 占据了不少时间片

模型这部分是最 trivial 的, 理论上知道了模型的架构都非常好写, 但实操的时候还是有不小的细节要注意, 特别是 TP (tensor-parallism) 相关的.

从最外层的角度来看, 一个 LLM (Llama 这种) 需要这些 layer:

Embedding layer (Embed)
Attention layer (Attn)
Feed forward network (FFN)

How to batch

在 LLM serving 中, 一个比较重要的问题是, 我们怎么进行 batching, 这决定了后面我们搭建的 model 的结构, 以及 scheduler 的预处理部分.

首先, 在 LLM online serving 的场景中, 我们会有很多的请求 (Req) 到来, 对于每个 Req, 它的输入是一些文字, 我们会首先把这些 text tokenize 变成 tokens, 类似一个 list of int.

在没有 batching 的时候, 我们只需要把输入 tokens 喂给模型, 每次把新生成的 token append 到之前的 tokens 后面, 然后把新的 tokens 一起喂给模型.

我们可以简单的把 LLM 看作一个 function $f$, 那么实际上我们输入就是 $x$, 输出 $y=f(x)$. 其中 $x$ 的维度是 $[\text{seq-len}]$, 每个元素的取值范围是 $0 \sim \text{vocab-size}$, $y$ 的维度是 $[1]$, 每个元素的取值范围同 $x$. 下一轮的输入就是把 $y$ 拼接到 $x$ 的后面, 维度是 $\text{seq-len} + 1$.

在有 batching 的时候, 传统 DL model 的做法是新增一个维度, 在我们的例子里就是输入 $x$ 的维度变成 $[2, \text{seq-len}]$. 但是在 LLM serving 中, 不同请求的输入的长度是不一样的. 这时候, 一个比较暴力的做法就是 padding, 即我们取输入长度为 $\max(\text{seq-len})$, 维度就是 $[2, \max(\text{seq-len})]$, 但这样几乎不可避免会带来一些计算上的浪费, 尤其是一些动态性非常强的 workload (既有长输入的请求, 也有短输入的请求).

这时候, 一个比较优雅的 solution 是: 我们把输入摊平. 假设输入有 $x1, \cdots, x_n$, 他们的长度分别是 $l_1, \cdots, l_n$, 那么我们把它拼起来, 直接合成一个大 $X$, 它的长度是 $\sum{i=1}^{n} l_i$. 这样, 我们就没有一点计算是多余的.

这个方法看起来很简单, 实际上会有一些工程上的 trick. 幸运的是, LLM 常见的 kernel, 大部分很容易就能支持这个操作. 比如矩阵乘法操作 $A \times B$, 本质上是对于 $A$ 的行向量和 $B$ 的每个列向量做内积. 这时候, 你把不同请求的矩阵 $A_i$, 沿着列的维度拼接起来得到形如 $[A_1^T, \cdots, A_n^T]^T$ 的 $A$, 那么 $A \times B$. 此时等价于对于每个 $A_i$ 分别做乘法, 即 $[A_1^T B, \cdots, A_n^T B]$, 这是分块举证告诉我们的.

唯一比较 tricky 的部分是 attention kernel. 它是一个取决于每个请求 tokens 数量的 kernel, 并不像 linear kernel, 没有良好的线性性质. 不过幸运的是, 伟大的 flash attention 和 flashinfer 都提供了类似 flash_attn_with_varlen 的接口, 支持直接用拼接起来的 $q, k, v$ 计算. 具体来说, 我们把沿着 $\text{seq-len}$ 维度拼起来的 $q, k, v$, 以及每一段的长度以特定格式喂给 flash attention 或者 flashinfer 的接口, 即可得到每个 query 对应的输出了.

因此, 我们的 batching 思路就非常简单: 首先选出一些请求, 然后把这些请求的 tokens 拼接起来, 直接作为模型的输入, 最后得到输出后再把结果拆开来. (当然实际上我们有 KV Cache, 因此我们只需要把每个请求不在 KVCache 中的那部分后缀 tokens, 对于 decode 每个请求的这部分 tokens 长度是 1).

Embedding Layer

首先分析单机的 Embedding layer. Embedding layer 的作用是, 把 tokenize 后的 ID (可以理解为 list of int) 转换为 embedding vector. 在单机上, 这其实就是一个根据 token ID 的值, 从一个 embedding vector list 中索引并且复制到输出的 tensor 里面.

import torch.nn.functional as F
# shape info:
# x: [n]
# weight [vocab_size, d]
# y: [n, d]
y = F.embedding(x, weight)
return y

在 TP 的时候, 我们的做法是把不同的 index 的 vector 分配到不同的机器上. 比如 TP=2 的时候, 我们会把前一半的 embedding vector 放在第一个 GPU 上, 后一半的 embedding vector 放在第二个 GPU 上. 假如我们要的 token id 比 $\frac{\text{vocab-size}}{2}$ 要小, 那么我们会从第一个 GPU 上取, 否则我们会从第二个 GPU 上取. 需要注意的是, 我们并没有切开 weight 的 $d$ 维度, 这也意味着每一个 vector 要么不在机器上, 要么就是完整的在一台机器上, 不会存在某个 token id 对应的 vector 横跨两台机器. 一个参考实现如下:

mask = (x >= vocab_start_idx) & (x < vocab_end_idx)
x = mask * (x - vocab_start_idx)
y = F.embedding(x, weight)
y = mask.unsqueeze(1) * y
all_reduce(y)
return y

在这段代码中, 每个 TP rank 存的是 $[\text{vocab-start-idx}, \text{vocab-end-idx})$ 这一段的 vector, 因此我们会 mask 掉其他的 embedding 操作, 对于不在当前 rank 的 indexing, 我们会将值 mask 为 0. 最后, 我们会对输出做 all reduce. 因此最后我们要的值一定存在且只存在于其中某个 rank 上, 所以最后的加和就是正确的 embedding 的值.

FFN

FFN 本质就是两个 linear 操作加上一个激活函数, 激活函数大部分也都是线性的, 所以这里仅讨论 linear 部分的处理, 即矩阵乘法. 在使用了摊平 batch 的方法后, 输入部分就是一个 $[n, d]$ 的二维矩阵. 对于非 TP 的情况, 我们直接用 torch 自带的 linear 函数即可.

import torch.nn.functional as F
# shape info:
# x: [n, d]
# up_proj [D, d]
# down_proj [d, D]
# y: [n, D]
# z: [n, d]
y = F.linear(x, up_proj)
z = F.linear(y, down_proj)
return y

需要注意的是, F.linear 传入的 weight 是一个事先就已经转置好的矩阵, 这样矩乘效率会更高一点.

在 TP 的时候, 我们每一层的输入输出在每个 TP rank 上都是一样且完整的 $[n, d]$. 在过 FFN 的时候, 我们会把 intermediate dimension $D$ 拆开 (一般来说 $D > d$, 所以叫做 up_projection 和 down_projection). 对于正常的 TP, 我们都会要求 GPU 总数量 $N$ 可以整除 $D$. 此时, 每个 $TP_rank$ 会持有一部分 up_proj $[\frac{D}{N}, d]$ 以及 down_proj $[d, \frac{D}{N}]$.

在经过 up_proj 之后, 每个 rank 只会持有一部分权重 $y_i$, 维度 $[n, \frac{D}{N}]$, 需要将所有 $GPU$ 的 $y$ 拼起来才能得到完整的 $y$. 但是, 为了减少通信次数, 我们可以将不完整的权重先过完 down_proj. 此时, 所有 rank 上得到的 $z_i$ 维度都是 $[n, d]$, 而根据分块矩阵乘法的知识可知, 此时完整的 $z$ 应该是所有的 $z_i$ 的和, 因此我们需要经过 all-reduce 操作. 这里的 all-reduce 是常见 collective operation 的一种, 详情可见 NCCL 对于 collective operation 的介绍.

下面是从 PyTorch 教程里面偷来的 Megatron 关于 TP 的 MLP (也就是 FFN) 的分析, 图比较直观, 读者可以自行用 $N = 2$ 的例子来验证最后输出的值 $Z$ 确实应该是 $\sum Z_i$, 这也是分块矩阵乘法告诉我们的.

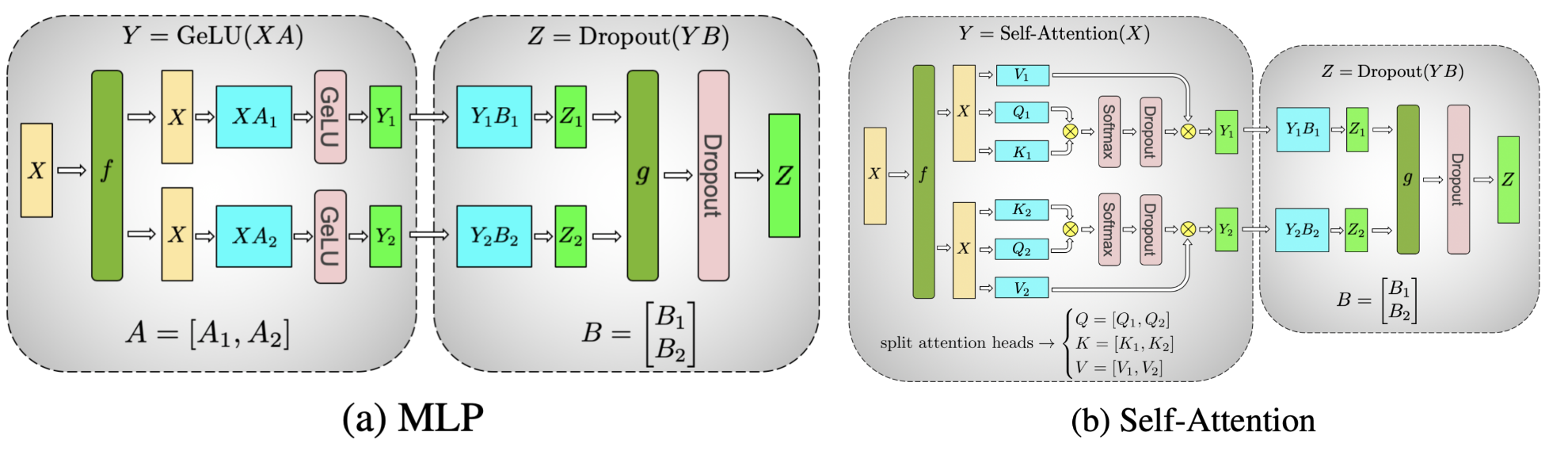
TP from megatron

Attention Layer

Attention 正如前面讲过的, 我们可以把 batch 里面的 $q, k, v$ 一起喂给对应的 flash attention 或 flashinfer 实现的 kernel, 这里我们把具体 kernel 实现叫做 attention backend.

KVCache

在 LLM serving 中, 一个重要的优化是 KV-Cache, 这是因为 causal masking 使得每个 token 的 $K$ 和 $V$ 只和过去的 token 有关.

具体来说, 为了生成第 $i$ 个 token, 我们需要过去的 $[q_i k_1, q_i k_2, \cdots, q_i k_i]$, 对它做 softmax 后, 再和 $[v_1, \cdots, v_i]$ 做内积. 实际我们依赖的是 $q_i$ 和 $k_1, \cdots k_n$ 和 $v_1 \cdots v_n$, 在这个过程中 $q_i, k_i, v_i$ 都是根据这轮输入新生成的. $k_i$ 和 $v_i$ 只会依赖过去的 token (i.e. 下标不超过 $i$ 的结果的影响), 因此我们可以把对应的 $k_i$ 和 $v_i$ 给 cache 起来.

这么讲可能会非常抽象, 笔者在这里强烈建议读者手推一下 KVCache 的原理, 本文就不过多赘述了.

如果你暂时不理解, 那也没关系. 作为一个 system 人, 你只需要知道: 完整的计算第 $i$ 个 token, 需要过去前 $i - 1$ 轮的 $k$ 和 $v$ 向量, 以及这一轮根据输入 token 新生成的 $ki$ 和 $v_i$ 和 $q_i$. 因此, 一个 naive 的 idea 就是: 我们可以把过去的 $k$ 和 $v$ 全部都收集起来. 在第一次收到一个长度为 $n$, 我们可以一口气生成 $k_1, \cdots, k_n$ 以及 $v_1, \cdots, v_n$. 在生成完第 $n$ 个 token, 开始生成第 $n + 1$ 个 token 的时候, 因为过去的 $k$ 和 $v$ 我们都 cache 住了, 我们只需要重新生成 $k{n+1}$, $q{n+1}$ 和 $v{n+1}$, 然后计算 attention.

可以看到, 我们现在计算 attention 分为了两个阶段:

预处理前 $n$ 个 token 的 $k$ 和 $v$, 同时生成第 $n$ 个 token.
生成新的 $k{n + 1}$ 和 $v{n+1}$, 同时生成第 $n + 1$ 个 token.

第一阶段就被称作 Prefill, 而第二个阶段被称作 Decode. 很显然, 第二个阶段的计算量要远远小于第一个阶段.

Paged KVCache

根据前文分析, 我们利用了 causal mask + attention 的数学性质, 可以用 KVCache 来加速生成 $token$. 我们也因此分成了 Prefill 和 Decode 两个阶段.

然而, 这带来了一些新的问题: decode 的时候, 常规的 attention 实现, 比如 flash_attn_with_varlen, 要求 $k$ 和 $v$ 存储是连续的. 但是我们 $k_i$ 和 $v_i$ 的时候都是一个一个生成的. 类比 C++, 我们每次会新增一个元素, 并且我们要求元素连续存储. 你会想到什么: std::vector! 只要用倍增的方法, 我们就可以解决了, 至多一倍的浪费.

但是呢, 事情并没有这么简单, 管理内存, 一个逃不开的问题就是: 内存碎片化. 一旦运行久了, 就容易出现碎片空余总和可能有 $n$ 那么多, 但你找不到一块连续的 $n$… 传统算法中有数不尽的相关 memory management 的 paper, 开源社区也有各种 malloc 实现, 问题看起来陷入死局.

事实上, 类似的 memory management 难题不仅在用户态程序存在, 对于操作系统 OS 也是存在的. 那么, OS 是怎么缓解这个问题的呢? 答案是 paging. 在通常的操作系统中, 我们给每个 4096 byte 对齐的连续空间称作一个 page, 然后会用页表来管理内存. 这样的好处是, 任何是 4096 整数倍的资源分配, 我们都可以保障 0 内存浪费. 同时, 页表也保证了 virtual address 看起来是连续的, 即使实际读写的 physical page 大概率并不连续.

笔者注: 实际维护 $N$ 个页的页表还有一个 O(N) 的表的开销, 但是它的开销反比于 page size, 因此服务器内存管理有时候也会借助 huge page, 一个 page 占 2M 甚至 1G, 来减小页表管理的 memory 和 TLB overhead.

这对我们的启发是, 我们也可以用 paging 的思想来节约显存 (GPU 的内存). 从硬件的角度, 我们可以修改 GPU 的 page table 实现. 当然, 调用硬件底层 API 很多时候相比软件方法还是会过于晦涩, 且不具有可拓展性. 在经典的 MLsys paper vLLM 中, 我们使用的就是软件管理的 paged KVCache. 具体来说, 我们一开始开好一个 memory pool, 在 attention kernel 里面读取 $ki$ 和 $v_i$ 的值的时候, 先通过一个 table $t$ 查找的 $k$ 和 $v$ 在 memory pool 中真实存储的位置, 这类似于一个二级索引操作, 即 $k{t[i]}$ 和 $v_{t[i]}$.

当然, 我们也可以自主调节 page size. 在 LLM serving 中, page size = $n$ 意味着对于任意 $n \cdot k, n \cdot k + 1, \cdots, n \cdot k + n - 1$, 这些 token 真实存储的位置必须是连续的. 不过, 在 LLM inference kernel 高度优化的今天, paging 带来的 overhead 以及可以几乎忽略不计了, 不同 page size 之间的性能差异已经很小了.

Radix KVCache

我们已经讨论了 KVCache, 以及 paged KVCache. 重新回顾一下 KVCache, 对于每个 $k_i$ 和 $v_i$, 它只会依赖于过去的 $k$ 和 $v$, 也就是由过去 $i$ 个 token 生成的 $k$ 和 $v$. 也就是说, 第 $i$ 个 $k_i, v_i$ 会依赖于第 $1, \cdots, i$ 个token.

那么, 我们是不是可以复用一些缓存呢? 既然每个 $k$ 和 $v$ 都是 condition on 它的前缀, 那么只要两个请求, 它们的前缀是一样的, 那么它们生成的 $k$ 和 $v$ 也一定是一样的. (不过输出之前, 需要 sampling, 会引入一些随机性, 导致生成的第 $i$ 个 token 对两个请求可能是不一样的). 这就是 Prefix Caching.

实际上, 我们都不需要前缀完全 match, 只要我们输入的前缀有一部分匹配到了过去某个请求前缀 tokens, 那我们就可以复用这部分. 例如, 假如一个请求前缀 tokens 是 $[0, 1, 2, 3]$, 过去某个请求的前缀 tokens 是 $[0, 1, 2, 4, 3]$, 那我们可以复用其中 $[0, 1, 2]$ 的部分, 从而尽可能减少计算量.

关于这一个优化, 一个比较著名的工作是 SGLang, 可惜居然没中 OSDI, 有点可惜.

TP attention

在标准的 TP 中, attention 的计算类似 FFN, 也会拆分到不同 rank 上. attention 的操作比较简单, 它的结果类似 FFN, 也是不同的部分和做 reduce (求和) 操作. 在这里, 我们是对不同的 attention head 计算出来的值作 reduce. 对于 GQA 的模型, 这里就要拆分 key-value head. 比如 Llama-3.1-70B 的模型有 8 个 key-value head, GQA ratio 是 8, 那么开启 TP=4, 就是每个 rank 负责 2 个 key-value attention 的计算 (GQA ratio 不会改变, 依然是每个 key-value attention 对应 8 个 query). 最后在每个 rank 都计算完后, 我们会执行 all-reduce, 把不同 rank 上的部分和都加起来.

Backend engine

后端的 engine, 对应的是 sglang 中的 TP worker. 一个 engine, 它需要做的事情就是执行 forward 操作. 当然, 现代的 LLM 往往还需要支持一些更加复杂的操作, 比如 cuda graph, 又比如 TP 的通信的初始化和管理, 还有 attention metadata 的处理, 以及模型权重的加载等杂七杂八的东西.

这里主要讨论两个, 一个是 attention metadata 的处理, 另一个是 cuda graph.